 |
相關閱讀 |
算算自己有多美——数学美才是真的美!
 |
>>> 民初教育及人才培養 >>> | 簡體 傳統 |
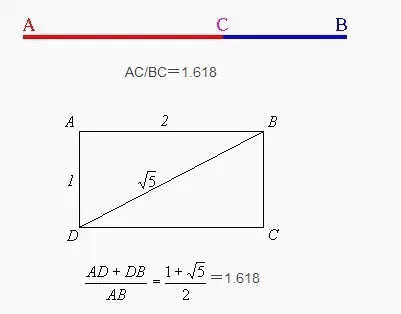
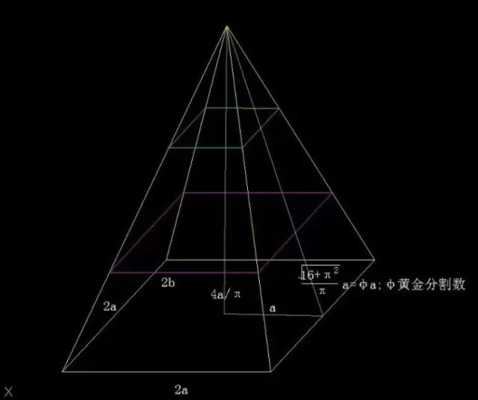
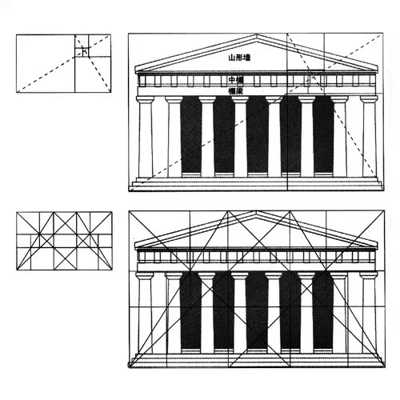
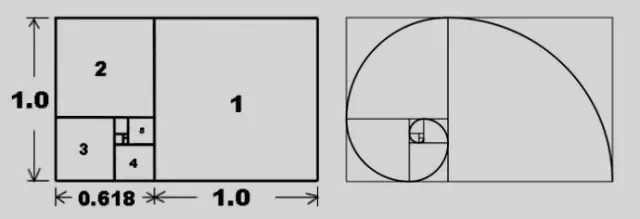
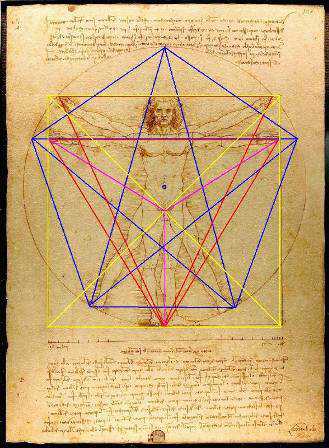
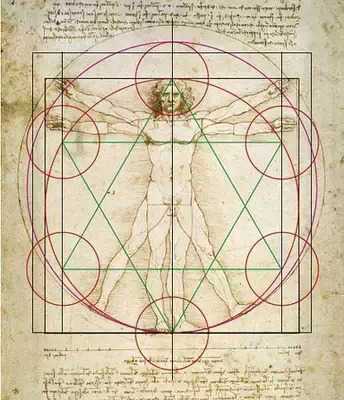
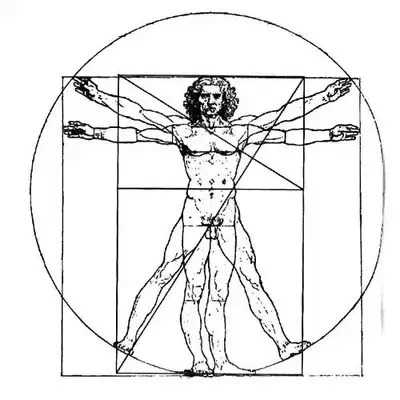
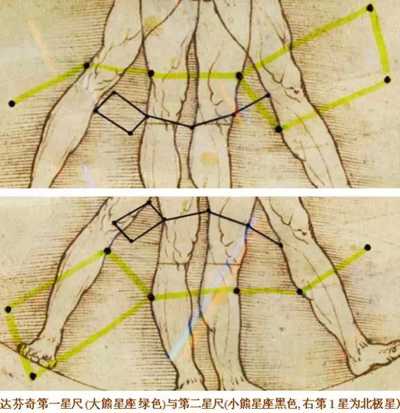
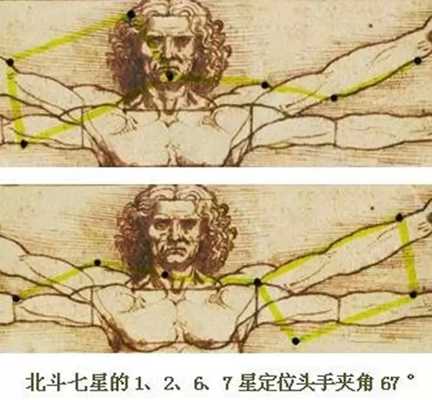
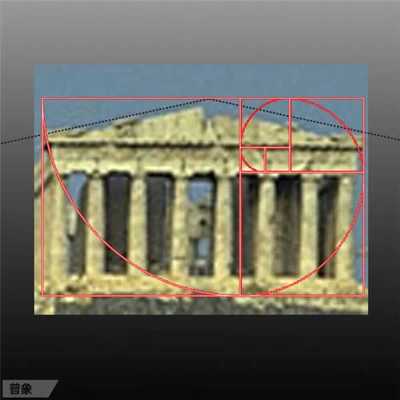
美的量化等式 我们生活的各方面似乎都可以被量化:人的膳食结构(包含热量,蛋白质,脂肪,碳水化合物,各种维生素,矿物质等等);体型(什么身高对应什么区间的体重);运动(建立有效的锻炼计划,实现相应指标)等等。如今,有些可穿戴设备也可以将我们的睡眠量化了,它可以计算出你的深浅度睡眠时间和呼吸频率。 这让我想到依靠大数据做出的电视剧《纸牌屋》,从角色安排到剧情发展,迎合观众的喜好制作,但是通过计算量化后的作品具有多大魅力?如果美也能被量化,必然就有这个等式: Beauty= b/a= (a+b)/b= 1.618... 相信大家在初中数学课上就学过这个公式了。简单来讲就是把一条线段一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值约为1∶0.618,即长段为全段的0.618。这个点就是黄金分割点,而0.618也被公认为最具有审美意义的比例数字,1∶0.618是最能引起人的美感的比例。黄金分割数也可以用希腊字母φ(拼音为“phi”,读作“fee”)表示。 关于黄金分割比例的起源大多认为来自毕达哥拉斯,据说在古希腊,有一天毕达哥拉斯走在街上,在经过铁匠铺前他听到铁匠打铁的声音非常好听,于是驻足倾听。他发现铁匠打铁节奏很有规律,这个声音的比例被毕达哥拉斯用数理的方式表达出来,被应用在很多领域。后来很多人专门研究过,开普勒称其为“神圣分割”,也有人称其为“金法”。 φ的应用 大自然中,树叶的叶脉,鹦鹉螺纹都具有黄金分割,这些是大自然作为造物主的杰作。而埃及人建造金字塔也应用了黄金分割,不过这早了毕达哥拉斯1000多年,可见那时候人们已从生活中发现这个奥秘也在应用,只是不明确这个规律。(当然关于金字塔是外星人的发射塔又是一说了。) 由于金字塔经历了常年的侵蚀,所以以下是理想化模型: 侧面倾斜角α,α=51.85°;正方形底面的底边为2个单位,这样,正四角锥体的高h,h=1.273;侧面的高H,H=1.6188,h≈√H H=1.6188≈Φ(1.618) 侧面的高(H)÷底边的1/2=1.6188÷[2x1/2]=1.6188≈Φ(1.618) 侧面的面积=1/2x2xH=1.6188 以正四角锥体的高h为边长的正四方形面积S,S=h2=1.620 即 1^2+h^2≈Φ^2(学好数理化,走遍天下都不怕!) 既然是美的等式 当然要用艺术品说话 断臂的维纳斯的肚脐 就是黄金分割点 大家不妨琢磨一下自己的肚脐。 重点来了! 矮个子女生根据这个可以算出 你应该穿多高的恨天高 才是黄金比例,才好看啊! 泰姬陵的正面 可以说把黄金分割用到了极致 帕特农神庙 也是建筑中运用黄金分割的典例 《最后的晚餐》中后墙和窗户 还有前景的桌子和弟子的脚 都存在着黄金分割 《蒙娜丽莎的微笑》 这样分析也是绝了 《维特鲁斯人》 画名是根据古罗马杰出的 建筑家维特鲁威(Vitruvii)的 名字取的 该建筑家在他的着作《建筑十书》中 曾盛赞人体比例和黄金分割 “维特鲁威人”是达芬奇 以比例最精准的男性为蓝本 这种“完美比例” 也即是数学上所谓的 “黄金分割” 对于这幅画,达芬奇自己阐述:建筑师维特鲁威斯在他的建筑论文中声言,他测量人体的方法如下:4指为一掌,4掌为一脚,6掌为一腕尺,4腕尺为一人的身高。4腕尺又为一跨步,24掌为人体总长。两臂侧伸的长度,与身高等同。从发际到下巴的距离,为身高的十分之一。自下巴至脑顶,为身高的八分之一。胸上到发际,为身高的七分之一。乳头到脑顶,为身高的四分之一。肩宽的最大跨度,是身高的四分之一。臂肘到指根是身高的五分之一,到腋窝夹角是身高的八分之一。手的全长为身高的十分之一。下巴到鼻尖、发际到眉线的距离均与耳长相同,都是脸长的三分之一。 人体中自然的中心点是肚脐。因为如果人把手脚张开,作仰卧姿势,然后以他的肚脐为中心用圆规画出一个圆,那么他的手指和脚趾就会与圆周接触。不仅可以在人体中这样地画出圆形,而且可以在人体中画出方形。即如果由脚底量到头顶,并把这一量度移到张开的两手,那么就会发现高和宽相等,恰似平面上用直尺确定方形一样。 此外,“维特鲁斯人”还有这些小秘密哦,只能说列昂纳多·达芬奇堪称艺术与科学巨匠。这里,还要提一个列昂纳多:列昂纳多·斐波那契。因为以他名字命名的斐波那契数列又称黄金分割数列,数列如下: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,
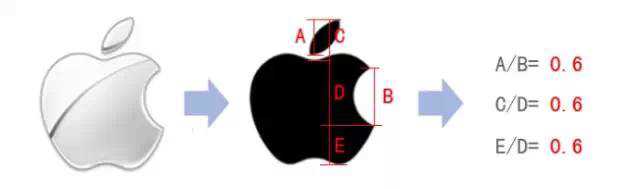
233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368......(特别指出:第0项是0,第1项是第一个1。这个数列从第二项开始,每一项都等于前两项之和。) 这样一个完全是自然数的数列,通项公式却是用无理数来表达的。而且当n趋向于无穷大时,前一项与后一项的比值越来越逼近黄金分割0.618.(或者说后一项与前一项的比值小数部分越来越逼近黄金分割0.618、前一项与后一项的比值越来越逼近黄金分割0.618) 最后,还有一个 丧心病狂的例子 Apple
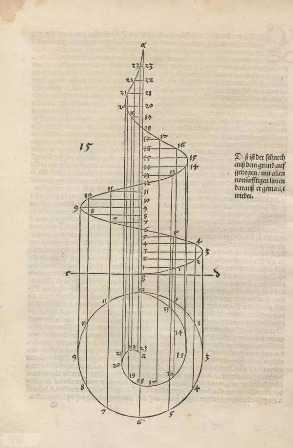
logo苹果中小叶子的高度和缺口的高度之比是0.6,而缺口的位置也和黄金分割有着千丝万缕的关系。还有以iphone4为例的主界面图标,拨号盘,甚至是色彩对比......艺点点们有兴趣可以多去发掘。 黄金分割的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方面也有着不可忽视的作用。甚至在股市研究,武器设计都有它的身影。当然把比例之美全归结它是不合理的,尽管物理学家霍金一直在寻找万物理论:一个统一的,简单的,优美的公式,但我相信美是绝不应该被量化的。 不过,话又说回来,用理性科学的角度去分析艺术品倒也是蛮有趣的,至少捣鼓了那么久,得出的一些结论还是符合大众思维和审美习惯的。一个等式可以简单粗浅地解释为什么美(符合认知习惯),却永远解释不了什么是美。 以下更多黄金分割经典案例来源于ArtTact 黄金分割其实是一组数列 1,1,2,3,5,8,13,21,34…… 相邻的两个数相加得出后一个 无限分裂延伸 没完没鸟~~ 请大家留意大卫像、帕特农神庙、蒙娜丽莎、埃及金字塔(内外高&其他各种参数)、墨西哥玛雅金字塔、DNA、各大星系、各种生物(螺类最明显),昆虫的复眼、…… 以下请看图,不解释。 这个流派有人信奉有人不信。但是过于迷信这些有理数或者无理数的神奇效果,我觉得是没啥必要的。用什么工具信奉什么理论不重要,重要的是你做出来的,得是个东西。 其它的也不多说了,我来讲一个丢勒 Albrecht Dürer 的故事。 丢勒是文艺复习时期最着名的德国画家和艺术理论家之一,(我认为他的最高成就在铜版画和木刻画)。 他写过几何学着作《度量四书》和《人体比例四书》,研究的几何结构包括螺旋线、蚌线、圆外旋轮线以及三维结构、多面体结构和倍立方,“偏爱托勒密的方法超过了欧几里德的方法”,非常有前瞻性地把几何学原理应用到建筑学、工程学和版式编排设计之中。 他曾经说过: 没有什么东西比一张毫无技巧笨拙的图片更让健全的判断力所讨厌了,尽管花费了许多心思和努力。现在这类画家没有意识到它们自身错误的唯一原因就是,他们没有学过几何学。没有几何学知识,任何人都不可能是成为一名纯粹的艺术家,但是应该谴责他们的老师,他们自己对这种艺术是无知的。——
丢勒 《Of the Just Shaping of letters》 1953 丢勒代表着“健全的判断力”蔑视你们这些无知的不配称之为艺术家的小瘪三们。是不是很耳熟。 但是,然而, although, but, however,
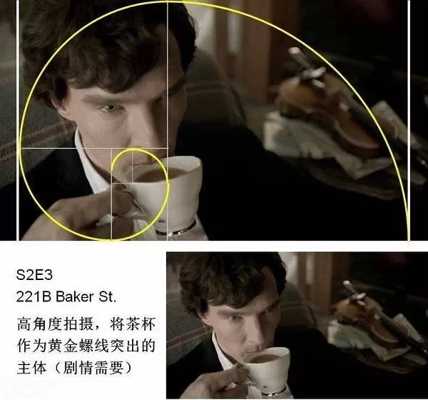
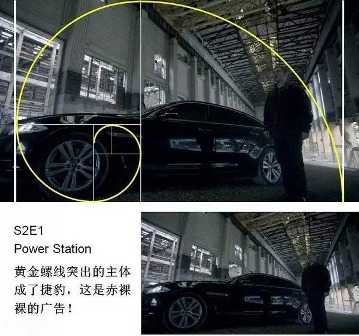
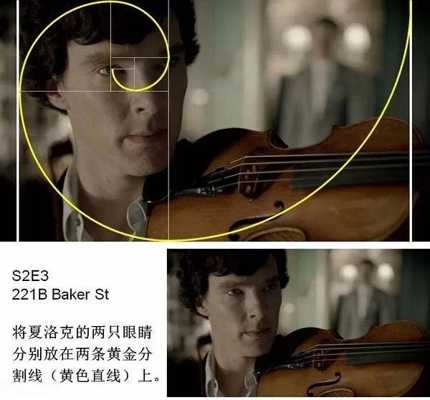
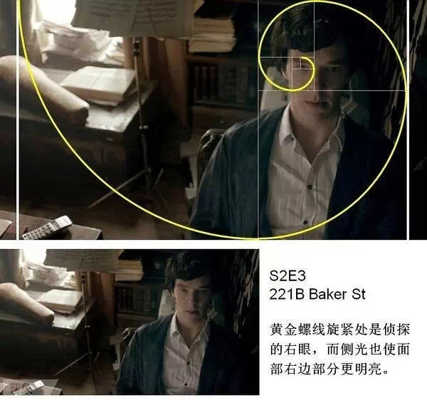
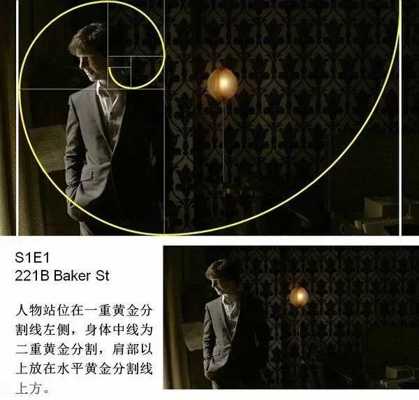
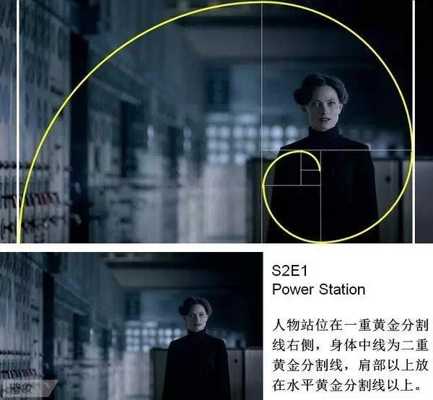
丢勒在死前的一篇附于他的几何艺术学着作的最后一卷书后的美学短文中,他写到: 一位艺术家应该凭借丰富的视觉经验去想象一个美的事物。一个人随手在半张纸上花一天的时间用铅笔画出的东西,或在一块小木头上刻出的东西,可能比另一个人花了一年的辛勤劳动炮制出来的大作品更有艺术魅力。 下面,我们用黄金比例来分析《神探夏洛克》画面构图: 转自艺术台 鸣谢 图文由公众号哲学园编辑











base
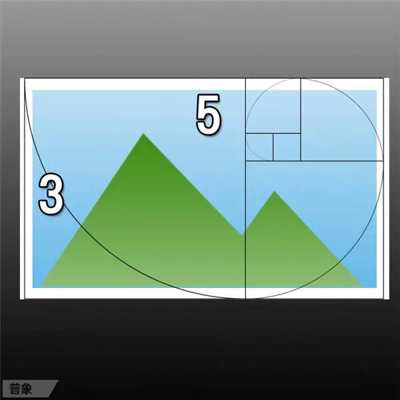
on这组数,我们发现,不仅是艺术,在大自然、宇宙、甚至人体构造中,艺术中也存着的黄金比例。例如:在生命密码DNA的两个扭曲螺旋结构组成中我们发现,螺旋之间的宽度和周长比例是0.618,也就是黄金定律,造就了人类潜意识中根深蒂固的审美模式,因此base
on这组数的都被称为“完美”~~




















文汇教育 2015-08-23 08:54:48
評論集
暫無評論。
稱謂:
内容:
返回列表

